Anthony Betancourt
Lab Partner: Josh Fofrich
Professor Wolf
Lab Performed: 08/31/2016
Free
Fall Lab
Part 1
Purpose:
This experiment is to demonstrate a free falling object, determining the value
of g, and to study the motion with the aid of an apparatus.
Procedure
1. Pull
a piece of the conductive tape through the bottom of the apparatus all the way
top keeping the paper “tight” with the weighted clip.
2. Turn
on power supply to electromagnet. Use
caution once apparatus is energized and do not touch any energized parts.
3. Prepare
wooden/metal cylinder for free fall by placing it under the electromagnet near
top of apparatus so it hangs.
4. Turn
on power to the spark generator.
5. Hold
down sparker switch on spark generator (generator sparks at 60 Hz leaving a dot
on the paper as it falls).
6. While
holding down the sparker button turn off the power source for the
electromagnet. Cylinder will fall once
power is turned off to electromagnet.
7. Turn
off power to the spark generator.
8. Tear
off paper strip and place on table top alongside a meter stick. Place the 0-cm mark on a dot and record the
position of each dot measured from the 0-cm mark.
9. Once
each dot is measured, open up Microsoft Excel and input measured values and
create a graph with trend line including R-value and equation of the line.
Theory
Utilizing the measured points on
the tape, which account for each second of free fall for the wooden cylinder, an
Excel spreadsheet can be made. Once a
reasonable number of data point are uploaded into Excel, the scatter plot of
data can be used to obtain a trend line and consequently derive the theoretical
value of g.
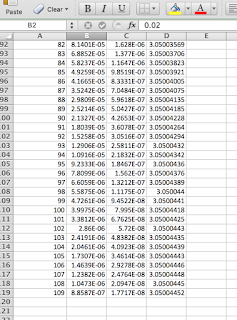
Measured Data
Graphs
(graph comparing mid-interval time with mid-interval
speed)
(graph comparing distance and time)
Analysis
1.
The velocity in the middle of a time interval is
the same as the average velocity for that same time interval.
For example, the time interval from 0.017
second to 0.050 seconds:
o 
o
Equation
from speed vs. Time graph trend line:
2.
Acceleration due to gravity can be calculated by
finding the area under the graph for speed vs. time.
3.
In order to find the acceleration using a
position vs. time graph, you must pick a point on the curve and find the 1st
derivative in order to find the velocity.
Then you take the second derivative of the function to find the
acceleration at that point.
Conclusion
Given the
relative accuracy of this experiment, the systematic errors in the procedures
hinder from obtaining a more precise value of g. These defects could be resultant of poor
measuring equipment, no taking into account any air resistance from the object
falling, any friction from the cylinder making contact with the apparatus, and
also the amount of data points entered into the spread sheet.
· 
The
experimental value of g should be within 10% of the accepted value. Luckily, the measurements taken along with
the number of data points that were recorded in the spreadsheet were able to
establish a good amount of data for the trend line graph. The more data points input into the computer,
the more accurate the experimental value of g will be. Along with more data points also utilizing
more precise measuring equipment can lead to greater accuracy.
Part 2: Errors and Uncertainty
1.
Every lab group’s value of g differed with one
being well below the accepted value.
Most
of the experimental values were just under the accepted value except one being
the actual accepted value. Subsequently, finding the exact value of g will vary
from group to group because one group might have more or less data point
collected from the tape measurements.
2.
Our group’s value of g ended up being the exact
same as the accepted value.
3.
Most of the class’s values were under the
accepted value for g.
4.
Our value might differ from the rest of the
class due to the amount of data points we input into the excel spreadsheet, the
accuracy of the measurements taken from the tape, or also accuracy of the
apparatus. Systematic errors involved in
the use of measurement instruments, equipment usage, and amount of data
collected. Random errors being those that
occur when human interaction occurs, such as the actual measuring of the tape, and
calculating uncertainty with the class averages.
5.
This lab focused on the ability for individuals
to work with others and run an experiment together in a timely manner with the
ultimate goal of proving one method of obtaining an experimental value of
g. Some key ideas focus on data acquisition
and making use of the measuring tools available to you. Also, the use of standard deviation in
calculating how replicable an experiment is to derive an expected value. One lesson learned is the proper method of
formally writing lab reports and documenting data to prove your result.